Find the inverse of f(x) = 3x/(x2) and check it Find the inverse of f(x) = 3x/(x2) and check itCalculate the inverse function of the given function simply by following the below given steps Let us take one function f (x) having x as the variable Consider that y is the function for f (x) Swap the variables x and y, then the resulting function will be x Now, solve the equation x Given the function f (x) f ( x) we want to find the inverse function, f −1(x) f − 1 ( x) First, replace f (x) f ( x) with y y This is done to make the rest of the process easier Replace every x x with a y y and replace every y y with an x x Solve the equation from Step 2 for y y
Inverse Functions Notes
The inverse of function f(x) = x^3 + 2 is mcq
The inverse of function f(x) = x^3 + 2 is mcq-The function f R → R defined by f(x) = 2x 1 is surjective (and even bijective), because for every real number y, we have an x such that f(x) = y such an appropriate x is (y − 1)/2 The function f R → R defined by f(x) = x 3 − 3x is surjective, because the preimage of any real number y is the solution set of the cubic polynomial An example of a function that is not injective is f(x) = x 2 if we take as domain all real numbers If we fill in 2 and 2 both give the same output, namely 4 So x 2 is not injective and therefore also not bijective and hence it won't have an inverse A function is surjective if every possible number in the range is reached, so in our case if every real number can be reached



1
Find the derivative of g(x) = 5√x by applying the inverse function theorem Hint g ( x) is the inverse of f ( x) = x 5 Answer g ( x) = 1 5 x − 4 / 5 From the previous example, we see that we can use the inverse function theorem to extend the power rule to exponents of the form 1 n, where n is a positive integer91 Inverse functions Informally, two functions f and g are inverses if each reverses, or undoes, the other More precisely Definition 911 Two functions f and g are inverses if for all x in the domain of g , f(g(x)) = x, and for all x in the domain of f, g(f(x)) = x Example 912 f = x3 and g = x1 / 3 are inverses, since (x3)1 / 3 = xAlgebra Examples Popular Problems Algebra Find the Inverse f (x)=x^32
Inverse of f (x)=x^26x I need to find the inverse of the function and and then from here I need to put the 2nd function in terms of y, however I do not know how to because of the function having the variable y twice I am not asking for the answer of the problem, only suggestions on which way to approach the situationThe equation (lo g 10 x 2 ) 3 (lo g 10 x − 1 ) 3 = (2 lo g 10 x 1 ) 3 has Number of real values of x satisfying x lo g 10 ( 1 2 x ) = x lo g 10 5 lo g 10 6 is Express each of the following in logarithmic form 1 0 − 3 = 0001A close examination of this last example above points out something that can cause problems for some students Since the inverse "undoes" whatever the original function did to x, the instinct is to create an "inverse" by applying reverse operationsIn this case, since f (x) multiplied x by 3 and then subtracted 2 from the result, the instinct is to think that the inverse would be to divide x
#19 Find the Inverse Function for f(x) = x^3 4An inverse function essentially undoes the effects of the original function If f (x) says to multiply by 2 and then add 1, then the inverse f (x) will say to subtract 1 and then divide by 2 If you want to think about this graphically, f (x) and its inverse function will be reflections across the line y = xClick here👆to get an answer to your question ️ The inverse function of f(x) = 8^2x8^2x8^2x8^2x∈ ( 1, 1) , is




Example 25 Let F X 4x 2 12x 15 Show That F Is Invertible




Form 4 5 Unit 1 Lesson 2 Inverse Function Brilliant Maths
The calculator will find the inverse of the given function, with steps shown If the function is onetoone, there will be a unique inverse Your input find the inverse of the function $$$ y=\frac {x 7} {3 x 5} $$$ To find the inverse function, swap $$$Finding inverse functions Learn how to find the formula of the inverse function of a given function For example, find the inverse of f (x)=3x2 Inverse functions, in the most general sense, are functions that "reverse" each other For example, if takes to , then the inverse, , must take to Or in other words,In mathematics, an inverse function (or antifunction) is a function that "reverses" another function if the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, ie, g(y) = x if and only if f(x) = y The inverse function of f is also denoted as As an example, consider the realvalued function of a real variable given by f(x



What Is The Inverse Function Of F X X 2 2x Quora



Inverse Function Of Y A X Q By Openstax Jobilize
The problem with trying to find an inverse function for \(f(x)=x^2\) is that two inputs are sent to the same output for each output \(y>0\) The function \(f(x)=x^34\) discussed earlier did not have this problem For that function, each input was sent to a different output A function that sends each input to a different output is called a oneFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor We were going over inverse functions in class and the method for mathematically finding an inverse function (ie replace y with x in the function and solve implicitly for y) I noticed, however, this method seemed impossible for a function such as f ( x) = x 3 x After trying for a while, I used the solve () function on my calculator to find




F2x 3 4x 9 Fx 3 2x 3 F X 3 2 X F 1 1 If Fx 2x 3 A Gauthmath




2 12 F R 3 2 R 10 X 1 3 2x G R 21 R 1o G X 1 X 2 H R 4 3 R 1 3 H X F O G X Verify If H X Is One To One And Onto If It Is Find The Inverse
The problem with trying to find an inverse function for f (x) = x 2 f (x) = x 2 is that two inputs are sent to the same output for each output y > 0 y > 0 The function f (x) = x 3 4 f (x) = x 3 4 discussed earlier did not have this problem For that function, each input was sent to aInverse Functions In mathematics, if two functions undo each other, then we say they are inverse functions, and we denote the inverse of a function f(x) as f1 (x)More technically, we have that52 Inverse Functions 381 y= f 1(x) exists, its graph can be obtained by re ecting y= x2 about the line y= x, in accordance with Theorem53 Doing so produces ( 2;4




Find The Inverse Of The Following Functions F R 0 Defined By F X 5 X



Inverse Of Square Root Function Chilimath
Free functions inverse calculator find functions inverse stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept inverse f\left(x\right)=x^{2}3 en Related Symbolab blog posts FunctionsPrevious Question Next Question _____ bytes are required to encode 00 bits of data, a) 1 b) 2 c) 3 d) 8 The function f(x) = x3 is bijection from R to RSome functions do not have inverse functions For example, consider f(x) = x 2 There are two numbers that f takes to 4, f(2) = 4 and f(2) = 4 If f had an inverse, then the fact that f(2) = 4 would imply that the inverse of f takes 4 back to 2 On the other hand, since f(2) = 4, the inverse of f would have to take 4 to 2




How To Find The Inverse Of A Function 4 Steps With Pictures




Inverse Functions Notes
To find the inverse of any function, first, replace the function variable with the other variable and then solve for the other variable by replacing each other An example is provided below for better understanding Example Find the inverse of f(x) = y = 3x − 2 Solution First, replace f(x) with f(y) Now, the equation y = 3x − 2 willThe function F is given by F (x)=x^26x13, for x>3 Look at my note to another student on completing the square and use it to write y = x 2 6x 13 in the form y = (xa) 2 b Solve this equation for x by writing (xa) 2 = y b and taking the squareF(x) has domain latex2\le x




Answered For The Function Y F X 3 2 A Find Bartleby




1 4 Inverse Functions Mathematics Libretexts
Inverse function Inverse functions are a way to "undo" a function In the original function, plugging in x gives back y, but in the inverse function, plugging in y (as the input) gives back x (as the output) If a function were to contain the point (3,5), its inverse would contain the point (5,3)If the original function is f(x), then its inverse f 1 (x) is not the same asThe function f is called invertible if there exists a function f −1 B → A with the domain B and the codomain A such that f −1(y) = x if and only if f (x) = y, where x ∈ A, y ∈ B The function f −1 is then called the inverse of f Not all functions have an inverse If a function f is not injective, different elements in its domainStart with the given function Replace f(x) with 'y' Switch x and y Subtract 2 from both sides Divide both sides by 3 Rearrange the equation So the inverse function is which is a function Start with the given function Replace f(x) with 'y' Switch x and y Add 5 to both sides Rearrange the equation Take the square root of both sides




41 Find The Inverse Function For F X 3 X 7 Youtube




25 Best Memes About Inverse Functions Inverse Functions Memes
Graphically, f(x) and f1 (x) are related in the sense that the graph of f1 (x) is a reflection of f(x) across the line y = xRecall that the line y = x is the 45° line that runs through quadrants I and III In addition, if f and f1 are inverse functions, the domain of f is the range of f1 and vice versa If the point (a, b) lies on the graph of f, then point (b, a) lies on the graph of f1F(x) is an exponent, same as logarithm You know the baseAsked in Mathematics by Afreen ( 307k points)




12x1 T05 01 Inverse Functions 10




Ex 1 3 6 Show F X X X 2 Is One One Find Inverse Of F
Question Find the inverse function of f f(x) = log3(x 2) (The three represents log base 3 of (x2) ) Found 2 solutions by josgarithmetic, jim_thompson5910 Answer by josgarithmetic() (Show Source) You can put this solution on YOUR website! Get an answer for 'Find the inverse function of f(x)=x^32?' and find homework help for other Math questions at eNotesSince the inverse is just a rational function, then the inverse is indeed a function Then the inverse is y = (–2x – 2) / (x – 1), and the inverse is also a function, with domain of all x not equal to 1 and range of all y not equal to –2 Find the inverse of f ( x) = x2 – 3 x 2, x < 15




Solved Please Help Are F X And G X Inverse Functions Across The Domain 3 Brainly Com



Solved Activity 1 Inverse Of A Function Determine Whether F And G Are Inverse Functions Using The Conditions That F G X X And G F X X F X Course Hero
Functions that have inverse are called onetoone functions A function is said to be onetoone if, for each number y in the range of f, there is exactly one number x in the domain of f such that f (xFind the inverse function f x 4 x 3 2 x 1 A f1 x x 3 2 x 4 B f 1 x 2 x 4 x 3 C from MATH General at Nonesuch School7 Important properties of a function and its inverse 1) The domain of f 1 is the range of f 2) The range of f 1 is the domain of f 3) (f 1o f) (x) = x for x in the domain of f 4) (f o f 1) (x) = x for x in the domain of f 1 5) The graphs of f and f 1 are reflection of each other on the line y = x



1



1
Solve the equation x^3 x y = 0, by Cardano's formulas, to get x in terms of y Since the derivative of x^3 x with respect to x is 3x^2 1, which is positive everywhere, where, there is a single value of x, for each given value of y The only d Onetoone functions So how do we prove that a given function has an inverse? Finding the Inverse of a Function Given the function f (x) f ( x) we want to find the inverse function, f −1(x) f − 1 ( x) First, replace f (x) f ( x) with y y This is done to make the rest of the process easier Replace every x x with a y y and replace every y y with an x x Solve the equation from Step 2 for y y




1 5 3 Inverse Function Example 3 Spm Additional Mathematics




Answered Find The Inverse Function Of F Bartleby
Functions −f and f 1 we −have to exchange x and y in the equation for f 1 So tocompare f ( x) = 2 √ its inverse we replace y 'sb and graph g f (x)= x f 1(x)=x2 y = x Figure 1 The graph of f−1 is the reflection of the graph of f across the line y = x In general, if you have the graph of a function f you can find the graph ofLet mathf(x) = x^3 x/math I'm assuming that mathf\mathbb{R}\to \mathbb{R} /math Since mathf(x)/math is a bijection mapping (the proof is very simple and I hope you know that) Therefore its inverse exists uniquely For finding the If f(x) = 4x3/6x4, x ≠ 2/3, then show that fof(x) = x for all x ≠ 2/3 What is the inverse of f?




The Domain Of The Function F X Sin 1 X 3 Sqrt 9 X 2 Is




Inverse Functions
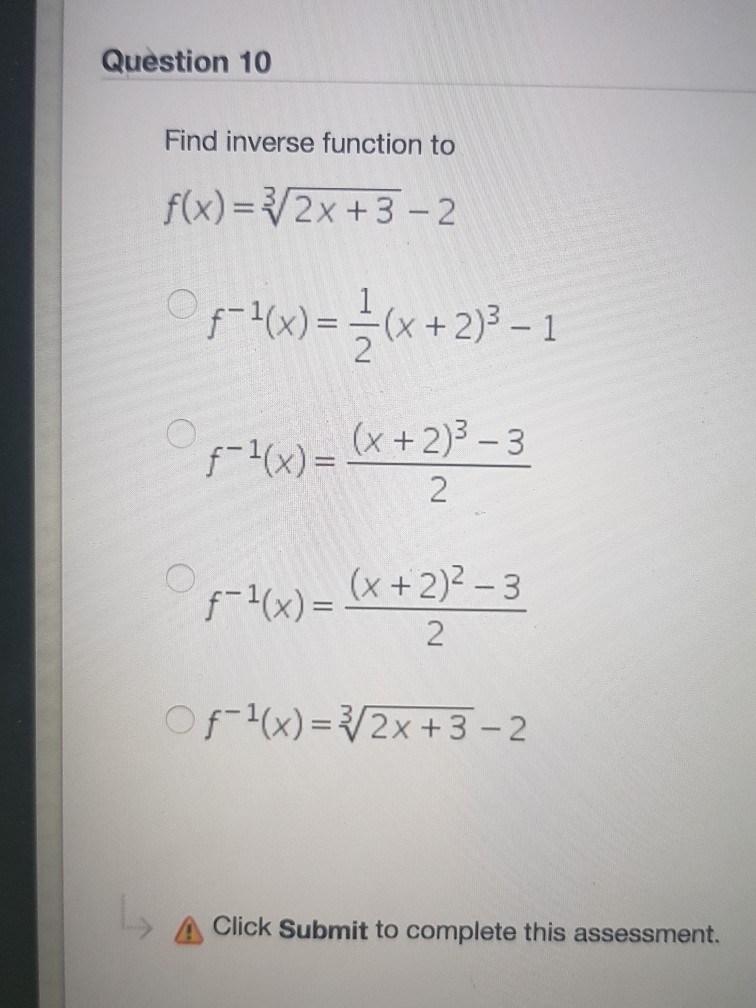



Question 10 Find Inverse Function To F X 2x 3 2 Chegg Com



Functions Inverse And Composite Functions
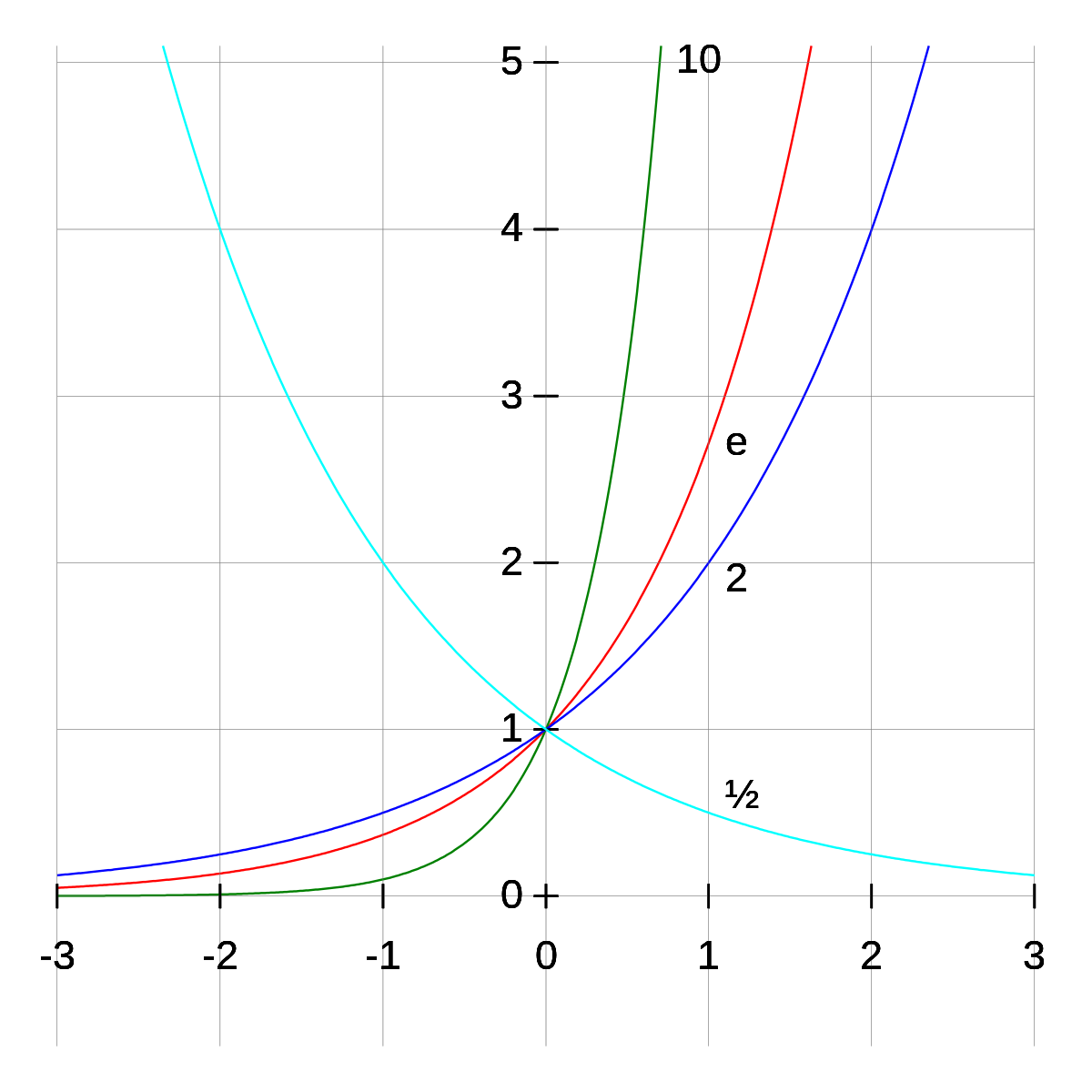



Exponentiation Wikipedia




Find The Inverse Function F Of The Function F Find The Range Of F And The Homeworklib




4 1 Inverse Functions T




How To Find Inverse Of Function In Different Cases Teachoo
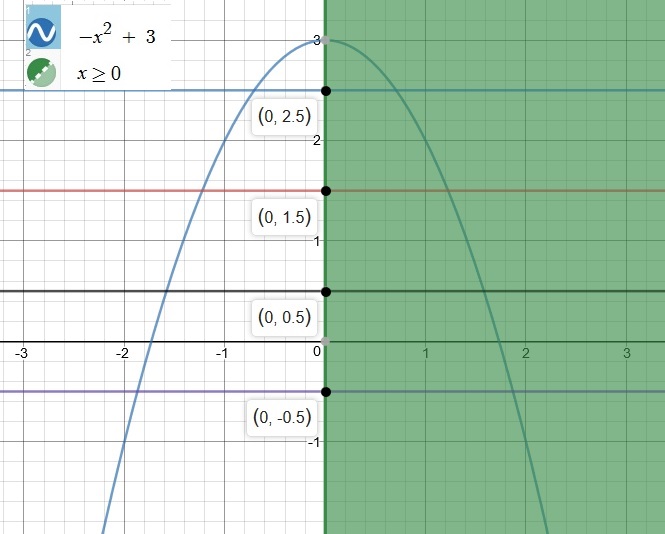



How Do You Graph F X X 2 3 X 0 And Then Use The Horizontal Test To Determine Whether The Inverse Of F Is A Function Socratic




Inverse Functions And Logarithms Pdf Free Download



Inverse Functions Practice Flip Ebook Pages 1 3 Anyflip Anyflip




Derivatives Of Inverse Functions



Show That The Function F In A R 2 3 Defined As F X 4x 3 6x 4 Is One One And Onto Hence Find F 1 Sarthaks Econnect Largest Online Education Community




Finding The Inverse Of A Function Complete Guide Mashup Math




Suppose F 1 Is The Inverse Function Of A Differentiable Function F And Let G X 1 F 1 X If F 3 2 And F 3 1 9 Find G 2




Derivatives Of Inverse Functions Example 2 On Vimeo




Ex 1 3 7 F X 4x 3 Show That F Is Invertible Cbse




If F R R Is Defined By F X X 3 Then F 1 8



Www Jensenmath Ca 2 6 inverse of a function worksheet solutions Pdf




Solution Manual Chapter 07 Exponential Logarithmic And Inverse T



What Is The Domain And Range For The Following Function And Its Inverse F X 3x 1 2 Mathskey Com
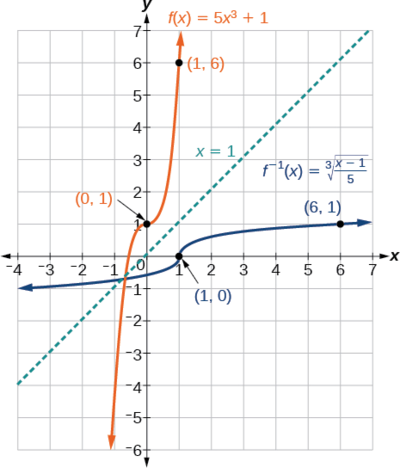



3 8 Inverses And Radical Functions Mathematics Libretexts



Www Lcps Org Cms Lib Va Centricity Domain March16 Block5 Pdf



Inverse Functions Practice Flip Ebook Pages 1 3 Anyflip Anyflip



Inverse Functions




Finding Inverse Functions Quadratic Example 2 Video Khan Academy




3 Ways To Find The Inverse Of A Quadratic Function Wikihow
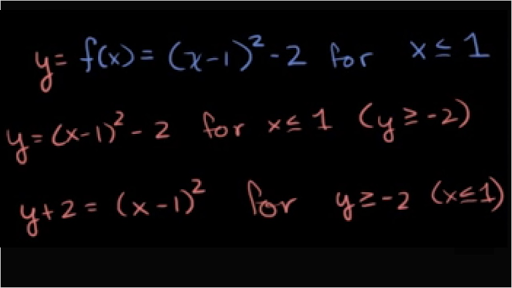



Finding Inverse Functions Quadratic Example 2 Video Khan Academy
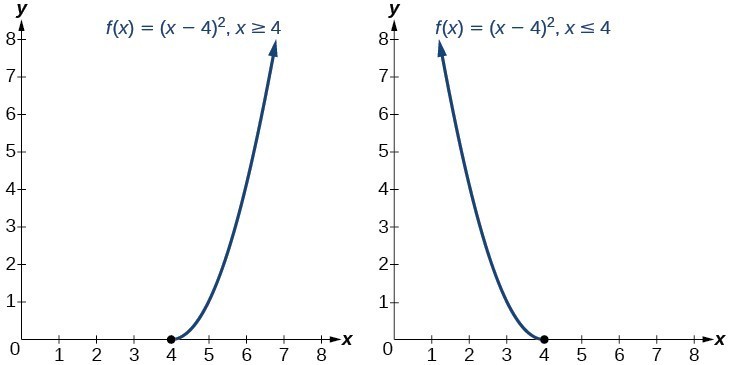



Restrict The Domain To Find The Inverse Of A Polynomial Function College Algebra




Find The Inverse Function Of F Informally F X X2 Chegg Com




Let F X 2x 3 X 3 If Function F One One And Onto Is F



Finding The Inverse Function Algebraically Expii



Q Tbn And9gcrua8gazszxaz61khbppkyqopanypswwu6ffytidvvwxm45rymg Usqp Cau



Lhsalgebra34 Weebly Com Uploads 3 1 3 8 Inverse Functions Worksheet Key Pdf




Let F R R Be Defined By F X X 3 3x 1 And G Be The Inverse Of F Then The Value Of G 5 Is Equal To




F X X 3 2 And G X 2x 3 Find Fog And Gof Is F Inverse G Maths Relations And Functions Meritnation Com



Http Www Wsfcs K12 Nc Us Cms Lib Nc Centricity Domain 7929 1 5 notes ans Pdf




Example 1 Find An Inverse Relation Find An
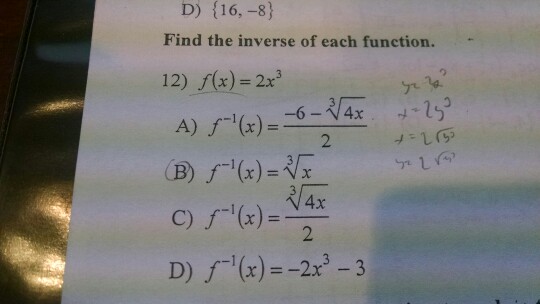



Find The Inverse Of Each Function 12 F X 2x 3 A Chegg Com



2



Solution Find The Inverse Of The Following Functions A G X 2x 3 4 X B F X Sqrt X 5 2




19 Find The Inverse Function For F X X 3 4 Youtube



Math Scene Functions 2 Lesson 6 Inverse Functions
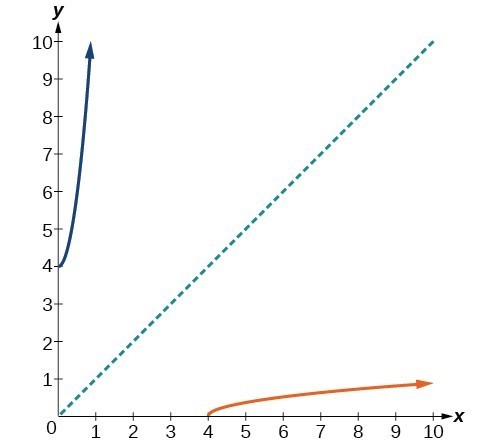



Restrict The Domain To Find The Inverse Of A Polynomial Function College Algebra




Inverse Of A Function In Math Tutorial Explaining Inverses Step By Step Several Practice Problems Plus A Free Worksheet With Answer Key




Inverse Functions The Inverse Of A Function Is Obtained By Interchanging The X And Y Values Of The Original Function Inverse Function Notation If The Ppt Download
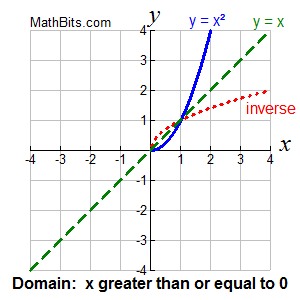



Inverse Functions Mathbitsnotebook A1 Ccss Math
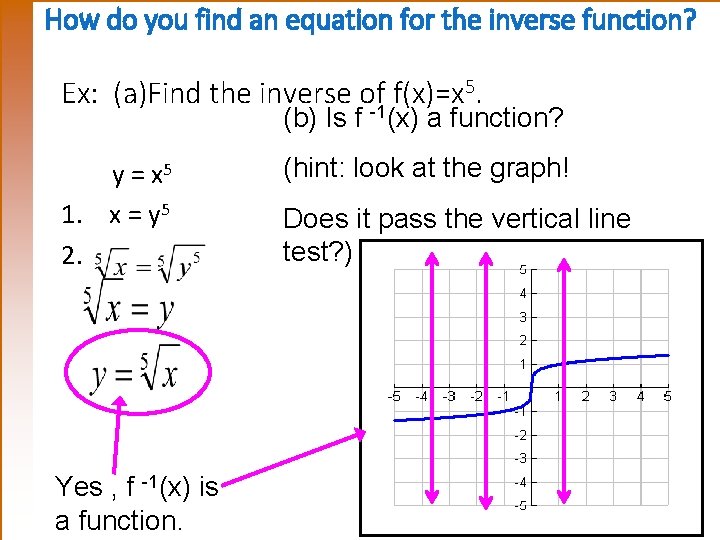



Warmup Given Fx 2 X 3 5 And




If 3 2 Is An Ordered Pair Of The Function F X Which Of The Following Must Be An Ordered Pair Of Brainly Com
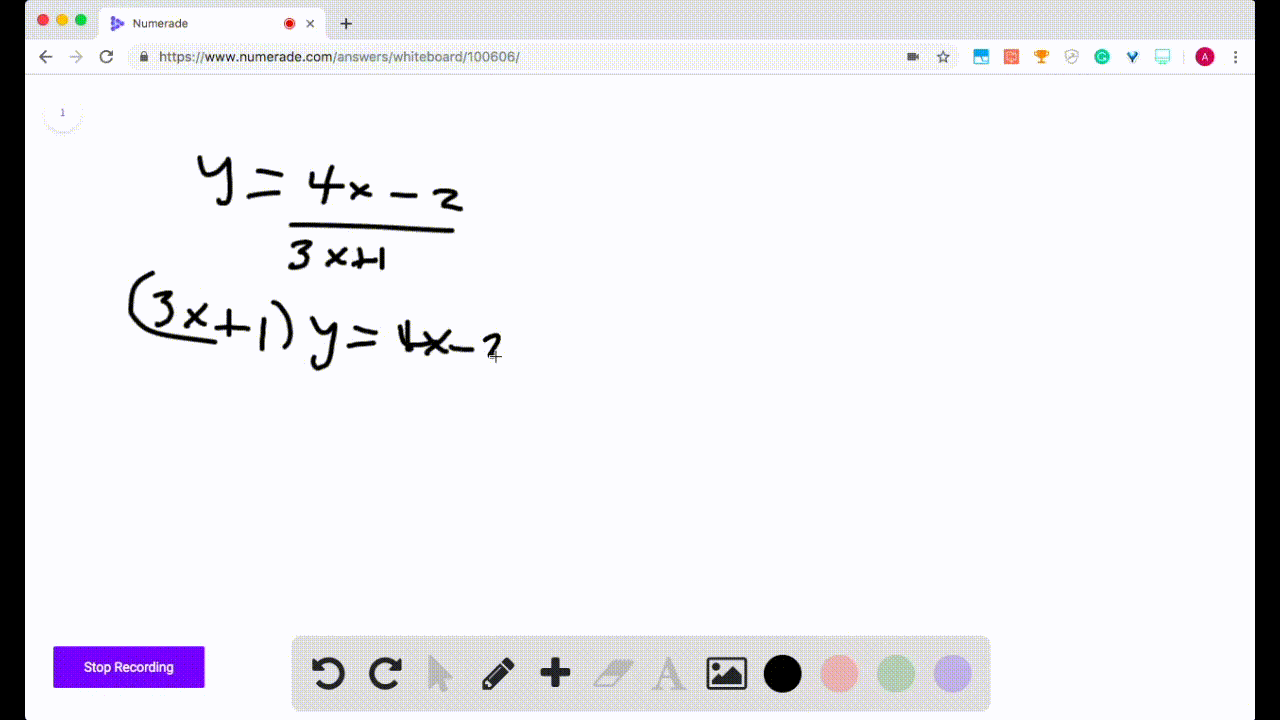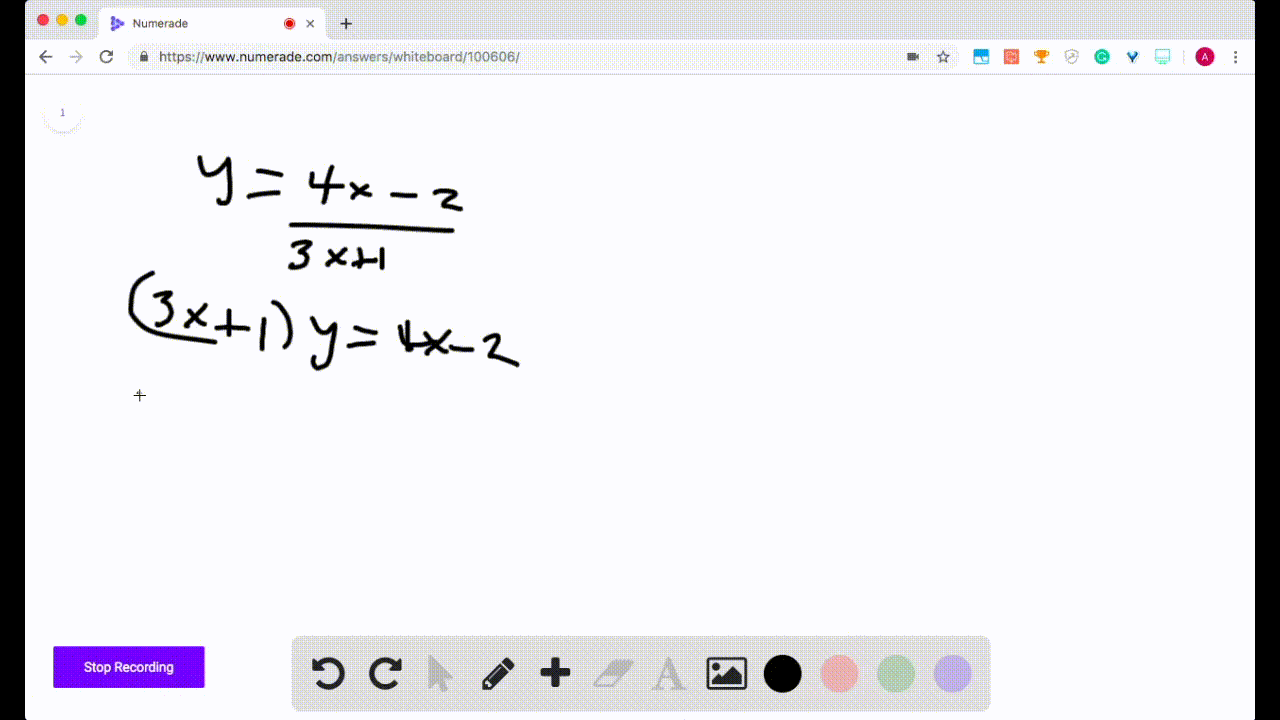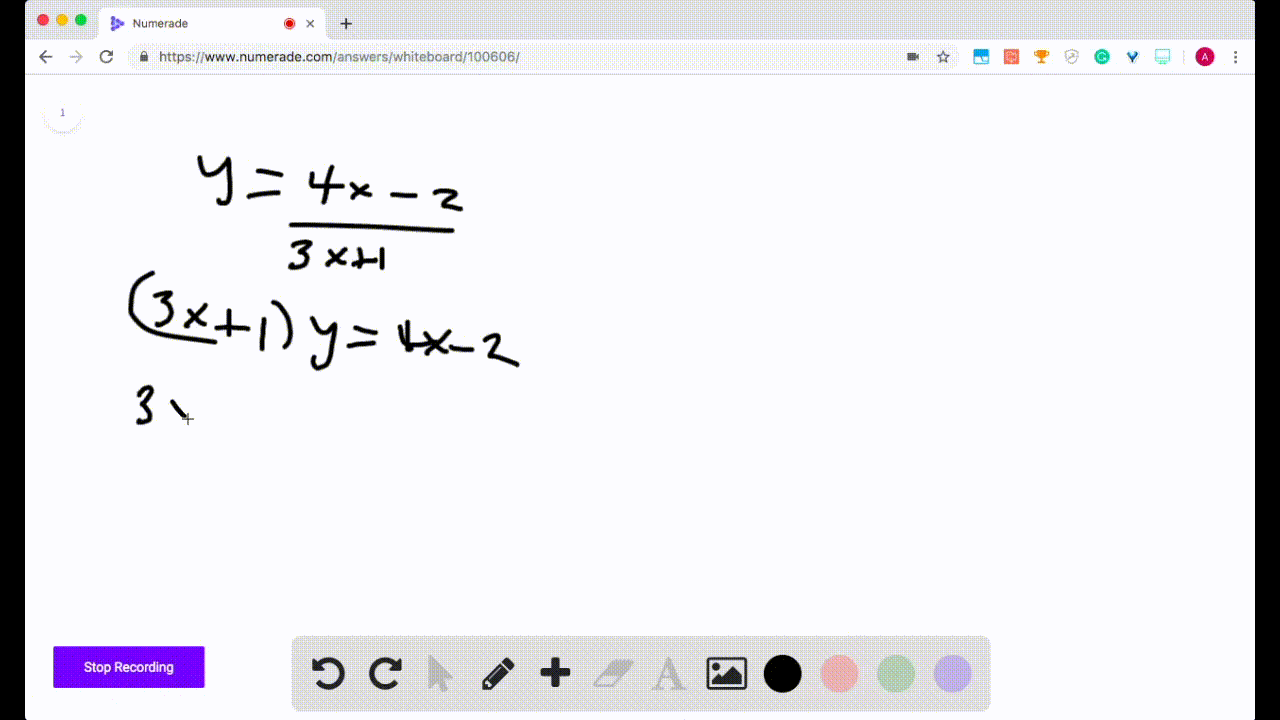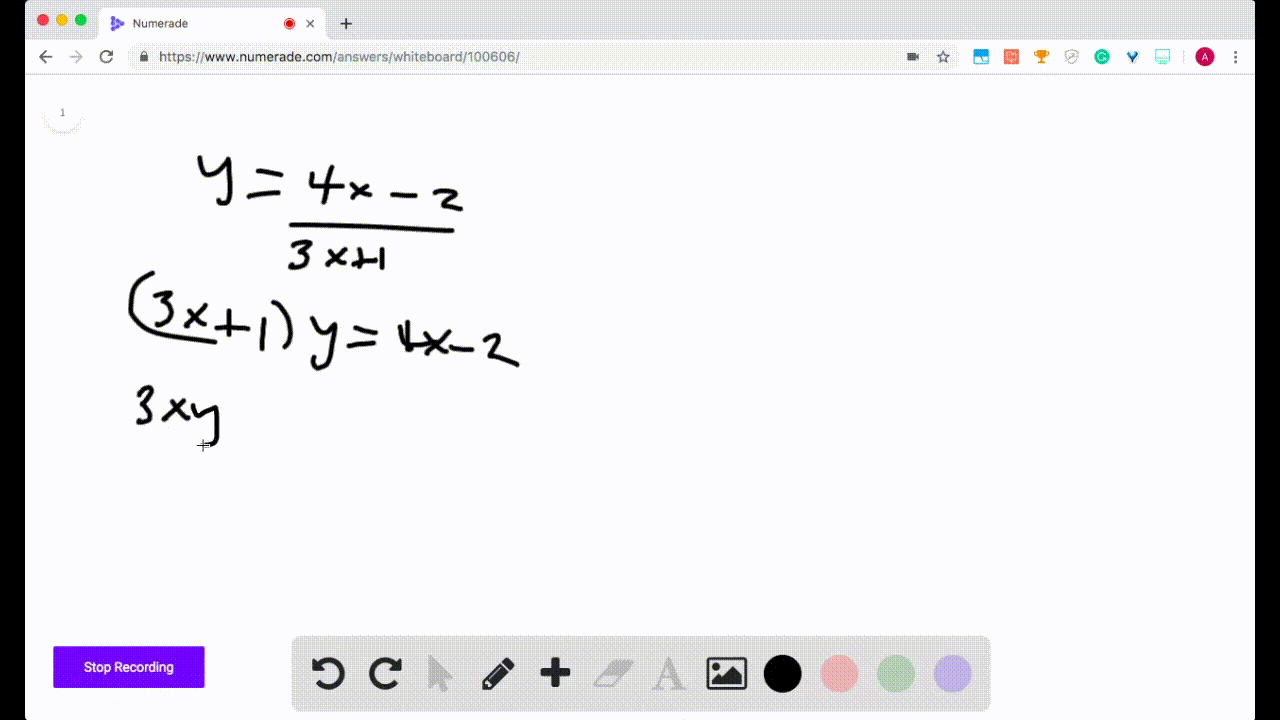



Solved Finding Inverse Functions Find The Inverse



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 3611 Answers inverse composition review0001 Pdf



Solved I Need Help How Does A Domain Restriction Placed On A Non Invertible Function Affect Its Inverse Course Hero




Show Function F X Y X 2 Y 2 2xy Is 1 1 By Inverse Function Theorem Mathematics Stack Exchange




Derivatives Of Inverse Functions From Equation Video Khan Academy



Proving That Two Functions Are Inverses Of Each Other



Math Scene Functions 2 Lesson 6 Inverse Functions




Finding The Inverse Function Algebraically Expii
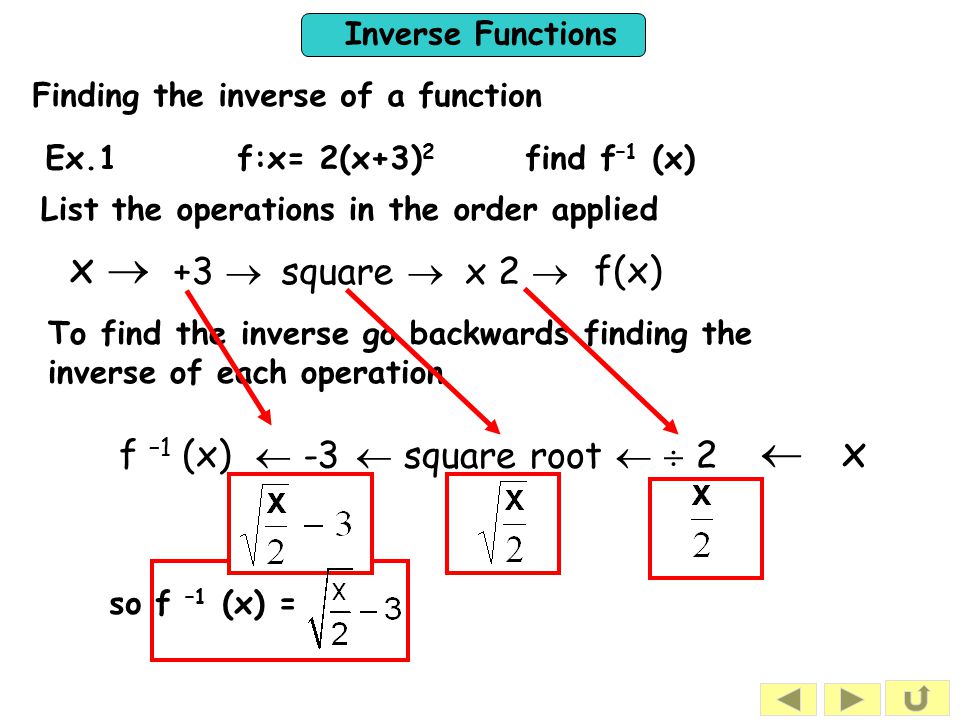



Inverse Functions C Christine Crisp Ppt Download
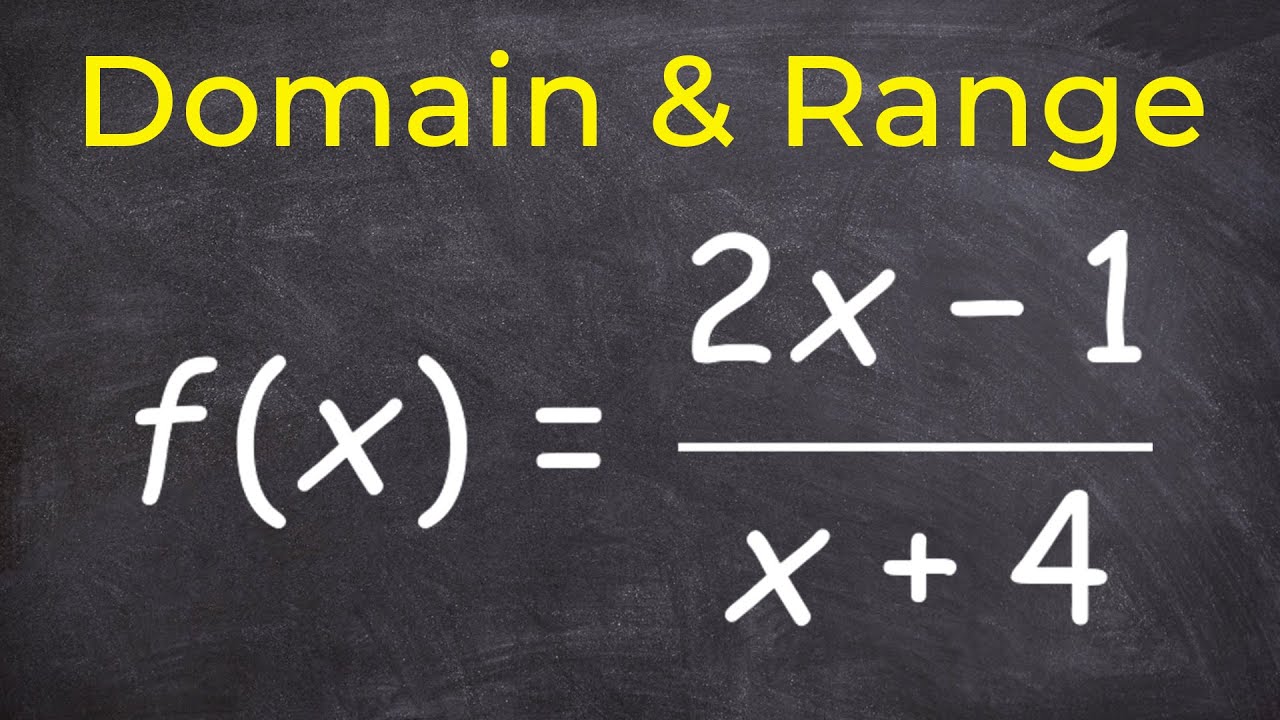



Finding The Inverse Of A Function Youtube




Inverse Derivative Problems Key




Inverse Of A Function In Math Tutorial Explaining Inverses Step By Step Several Practice Problems Plus A Free Worksheet With Answer Key




Inverse Of Rational Function F X 2 X 3 Youtube




Downloaded From Equations 2 4 The Reciprocal Function X 1 X Pdf Free Download




Inverse Function Wikipedia




Inverse Functions Ppt Download
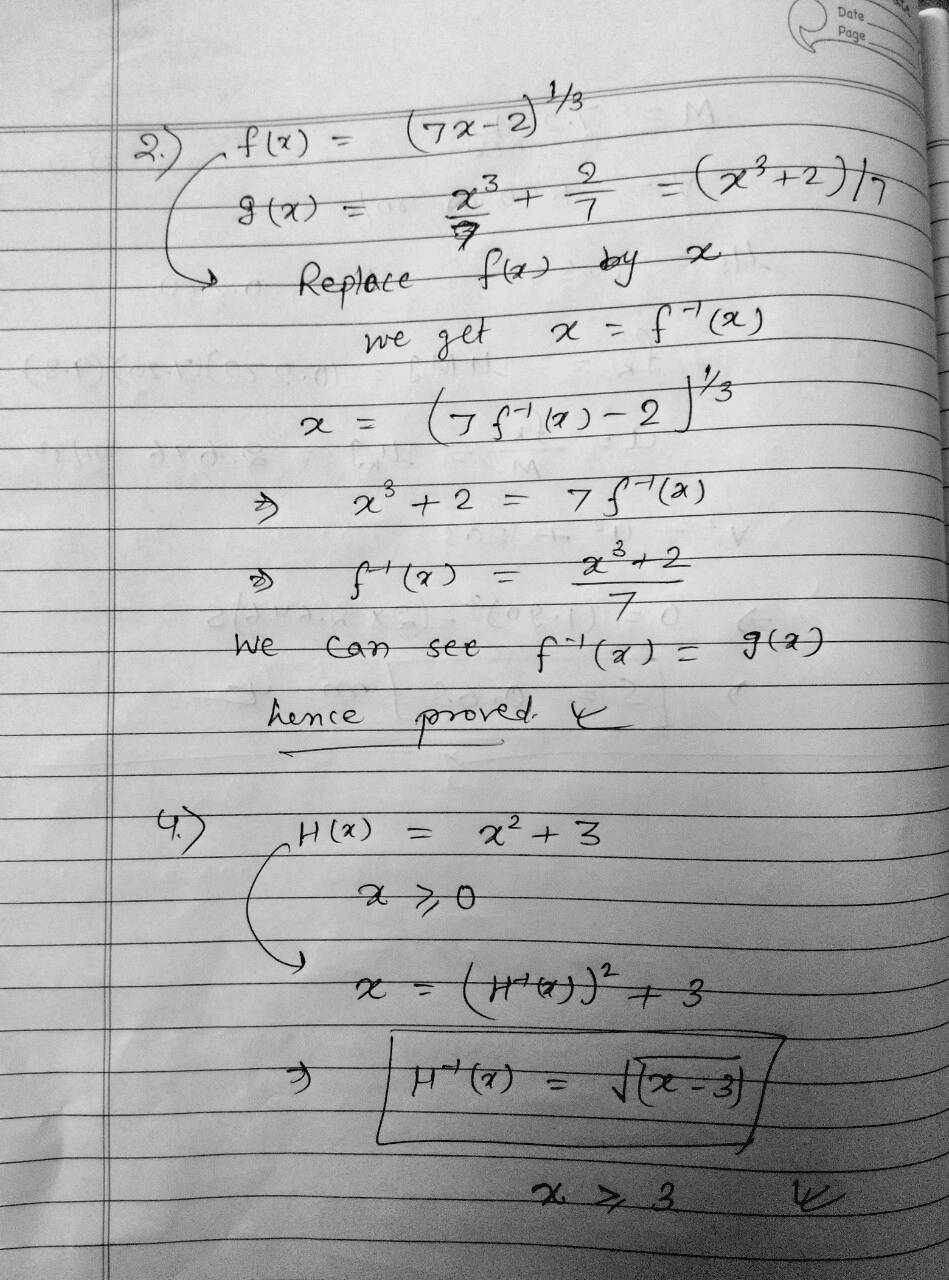



Oneclass 2 Show That F X 3 Sq Root 7x 2 And G X X 3 2 7 Are Inverses 4 Find The Invers



What Is The Formula For The Inverse Function F X 2x 3 2 X Quora
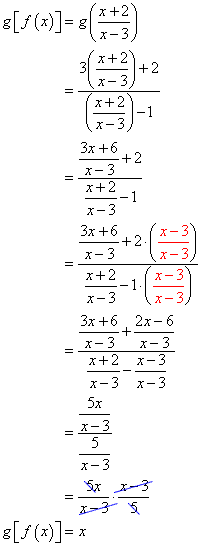



Verifying If Two Functions Are Inverses Of Each Other Chilimath




View Question Given The Function F X X 1 X 3 Find The Inverse Of F X Use Parenthesis To Type Your Answer



Biomath Functions




1 Find The Inverse Of The Function F X 3 5 Points Chegg Com




Unit 1 Functions Minds On Unit 1 Functions Lesson 5 Inverse Functions Example Find The Inverse Of F X X 3 Ppt Download




2 7 Summary Functions Siyavula



Solution Find The Inverse Of The Function F X X 1 3 2 I Am So Confused Can Someone Please Help Me Fr A X 2 3 B X 1 3 2 C Y 2 3 D Doesn 39 T Exist



What Is The Inverse Of F X 3 4x 2 If It Is A 1 1 Function Quora



Inverse Functions Test
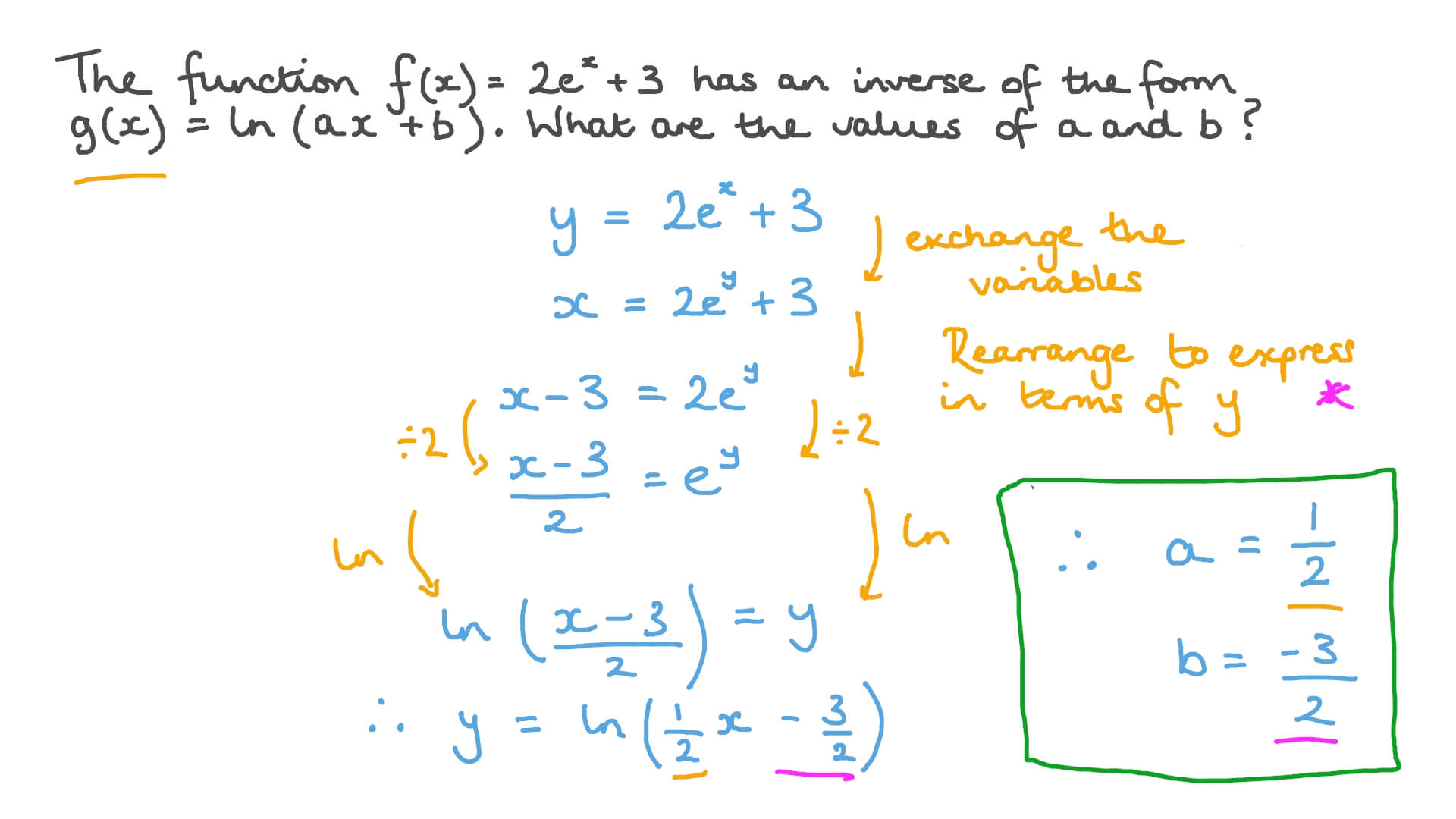



Question Video Finding The Inverse Of A Function Containing An Exponential Function Nagwa




Find The Inverse Function F 1 X For F X 3 2 Chegg Com



Inverse Functions



1




Homework 3 Solutions Introduction To Discrete Structures Cot 3100 Docsity




Inverse Functions Solutions Examples Videos



0 件のコメント:
コメントを投稿